Podemos utilizar la regresión lineal en Excel como herramienta estadística que se utiliza como modelo de análisis predictivo para verificar la relación entre dos conjuntos de datos de variables.
Usando este análisis, podemos estimar la relación entre dos o más variables para realizar pronostico de ventas. Podemos ver dos tipos de variables, es decir, «variable dependiente y variable independiente».
- La variable dependiente es el factor que estamos tratando de estimar.
- La variable independiente es lo que influye en la variable dependiente.
Entonces, usando Regresión lineal en Excel, podemos ver cómo la variable dependiente experimenta cambios cuando la variable independiente cambia y nos ayuda a decidir matemáticamente qué variable tiene un impacto real.
¿Cómo agregar la herramienta de análisis de datos de regresión lineal en Excel?
La regresión lineal en Excel está disponible en el paquete de herramientas de análisis , que es una herramienta oculta en Excel. Esto se puede encontrar en la pestaña Datos.
Esta herramienta no es visible hasta que el usuario la habilita. Para habilitar esto, siga los pasos a continuación.
1: Vaya a ARCHIVO >> Opciones.

2: Seleccione » Complementos de Excel » en Administrar lista desplegable en Excel y haga clic en «Ir».
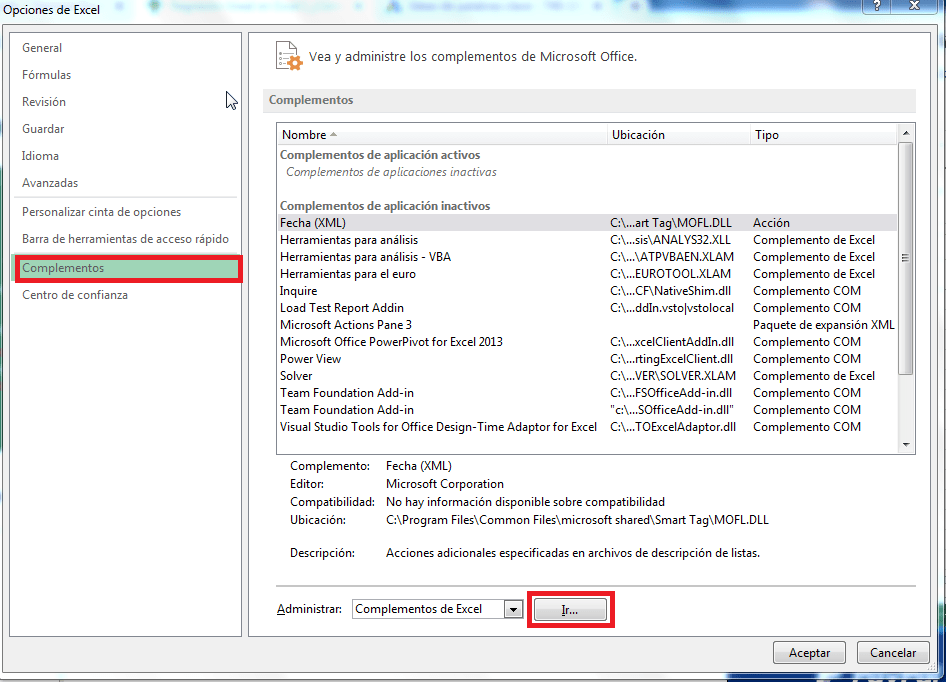
3: Marque la casilla «Paquete de herramientas de análisis» en los «Complementos».
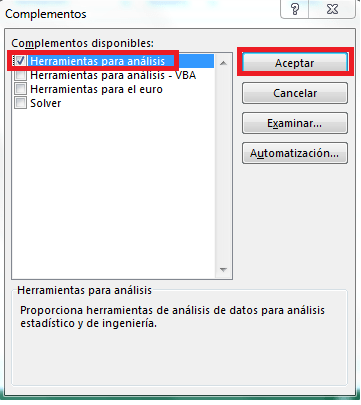
Ahora deberíamos ver la opción «Paquete de herramientas de análisis» en la pestaña «Datos».

Con esta opción, podemos realizar muchas opciones de «análisis de datos». Veamos el ejemplo ahora.
Ejemplos de Regresión lineal en excel
Como dije, Excel de regresión lineal consta de dos cosas, es decir, «variables dependientes e independientes». En este ejemplo, vamos a hacer una regresión lineal simple en Excel.
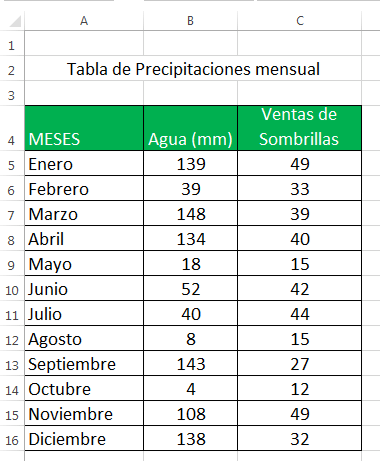
Lo que tenemos es una lista de la precipitación mensual promedio durante los últimos 12 meses en la columna B, que es nuestra variable independiente (predictor), y el número de sombrillas vendidas en la columna C, que es la variable dependiente. Por supuesto, hay muchos otros factores que pueden afectar las ventas, pero por ahora nos enfocamos solo en estas dos variables:
Con Análisis de datos agregado habilitado, lleve a cabo estos pasos para realizar análisis de regresión en Excel:
- En la pestaña Datos , en el grupo Análisis , haga clic en el botón Análisis de datos.

2. Seleccione Regresión y haga clic en Aceptar.
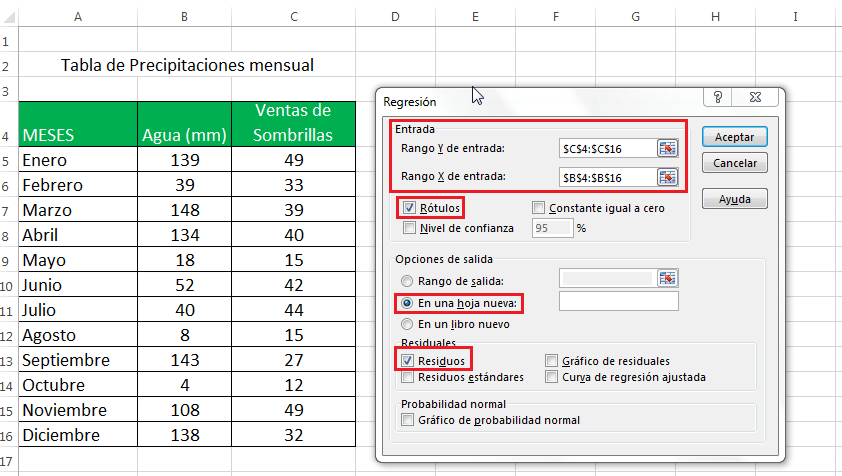
3. En el cuadro de diálogo Regresión , configure los siguientes ajustes:
Seleccione el rango de entrada Y , que es su variable dependiente . En nuestro caso, se trata de ventas generales (C4: C16).
Seleccione el rango de entrada X , es decir, su variable independiente . En este ejemplo, es la precipitación mensual promedio (B4: B16).
Si está creando un modelo de regresión múltiple, seleccione dos o más columnas adyacentes con diferentes variables independientes.
Marque la casilla Etiquetas si hay encabezados en la parte superior de sus rangos X e Y.
Elija su opción de Salida preferida , una nueva hoja de trabajo en nuestro caso.
Opcionalmente, seleccione la casilla de verificación Residuales para obtener la diferencia entre los valores predichos y reales.
4.Haga clic en Aceptar y observe el resultado del análisis de regresión creado por Excel.
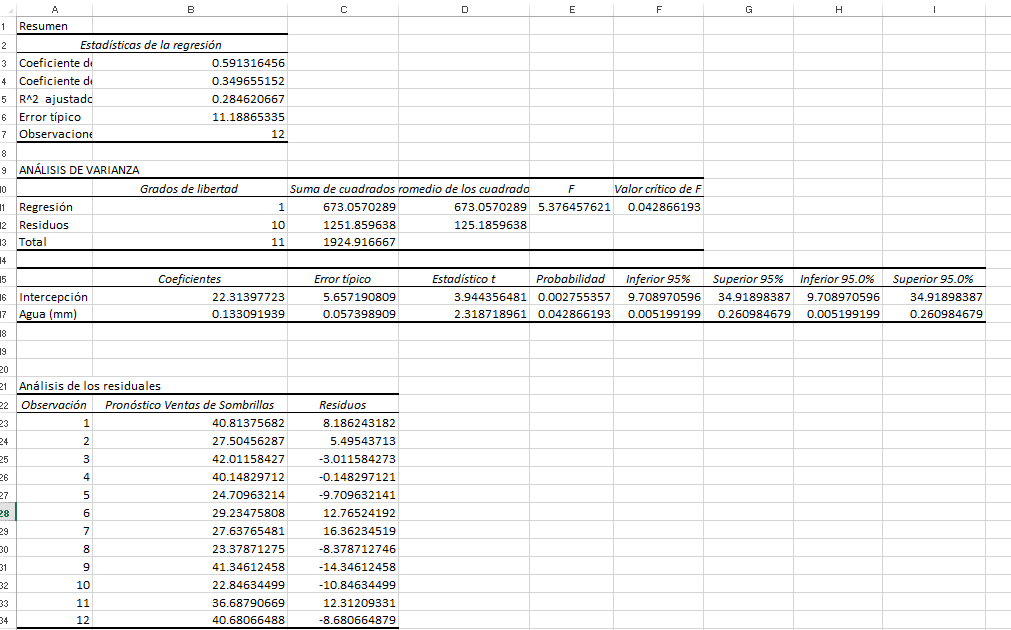
Interpretar el resultado del análisis de regresión
Como acaba de ver, ejecutar la regresión en Excel es fácil porque todos los cálculos se realizan automáticamente. La interpretación de los resultados es un poco más complicada porque necesita saber qué hay detrás de cada número. A continuación, encontrará un desglose de 4 partes principales del resultado del análisis de regresión.
Salida del análisis de regresión: Salida resumida
Esta parte le indica qué tan bien se ajusta la ecuación de regresión lineal calculada a sus datos de origen.

Coneficiente de correlación múltiple. Es el coeficiente de correlación que mide la fuerza de una relación lineal entre dos variables. Puede ser cualquier valor entre -1 y 1, y su valor absoluto indica la fuerza de la relación. Cuanto mayor sea el valor absoluto, más fuerte será la relación:
1 significa una fuerte relación positiva
-1 significa una fuerte relación negativa
0 significa que no hay ninguna relación
Coeficiente de determinación R2. Se utiliza como indicador de la bondad del ajuste. Muestra cuántos puntos caen en la línea de regresión. El valor R 2 se calcula a partir de la suma total de cuadrados, más precisamente, es la suma de las desviaciones cuadradas de los datos originales de la media.
En nuestro ejemplo, R 2 es 0.34 (redondeado a 2 dígitos), lo que no es bueno. Significa que el 0.34% de nuestros valores se ajustan al modelo de análisis de regresión. En otras palabras, el 34% de las variables dependientes (valores de y) se explican por las variables independientes (valores de x). Generalmente, una R al cuadrado de 59%.
Cuadrado R ajustado. Es el cuadrado R ajustado por el número de variable independiente en el modelo. Querrá usar este valor en lugar de R cuadrado para análisis de regresión múltiple.
Error estándar. Muestra la precisión de su análisis de regresión: cuanto menor es el número, más seguro puede estar acerca de su ecuación de regresión.
Observaciones. Es simplemente el número de observaciones en su modelo.
Salida del análisis de regresión lineal:
La segunda parte del resultado es Análisis de varianza:

Básicamente, divide la suma de cuadrados en componentes individuales que brindan información sobre los niveles de variabilidad dentro de su modelo de regresión:
Grados de liberación: es el número de grados de libertad asociados con las fuentes de varianza.
Suma de cuadrados: es la suma de cuadrados, cuanto menor sea el SS residual en comparación con el SS total, mejor se ajustará su modelo a los datos.
Promedios de los cuadrados: es el cuadrado medio.
F es el estadístico F o prueba F para la hipótesis nula. Se utiliza para probar la importancia general del modelo.
La significancia F es el valor P de F.
La parte de Análisis de varianza rara vez se usa para un análisis de regresión lineal simple en Excel, pero definitivamente debe observar de cerca el último componente. El valor de Significancia F da una idea de cuán confiables (estadísticamente significativos) son sus resultados. Si la significancia F es menor que 0.05 (5%), su modelo está bien. Si es mayor que 0.05, probablemente sea mejor que elija otra variable independiente.
Resultado del análisis de regresión lineal: coeficientes
Esta sección proporciona información específica sobre los componentes de su análisis:

El componente más útil de esta sección son los coeficientes . Le permite crear una ecuación de regresión lineal en Excel:
y = bx + a
Para nuestro conjunto de datos, donde y es la cantidad de paraguas vendidos yx es una precipitación mensual promedio, nuestra fórmula de regresión lineal es la siguiente:
Y = Coeficiente agua (mm) * precipitación mensual (x variable) + coeficiente Intercepción
Equipado con valores ayb redondeados a tres decimales, se convierte en:
Y=0.13309*x+22.314
Por ejemplo, con una precipitación mensual promedio igual a mm, las ventas de paraguas serían aproximadamente 40.8:
0.13309*139+22.314=40.8
De manera similar, puede averiguar cuántos paraguas se venderán con cualquier otra precipitación mensual (x variable) que especifique.
Salida del análisis de regresión lineal en excel: residuos
Si compara el número estimado y real de paraguas vendidos correspondientes a la precipitación mensual de 139 mm, verá que estos números son ligeramente diferentes:
Estimado: 40.8 (calculado anteriormente)
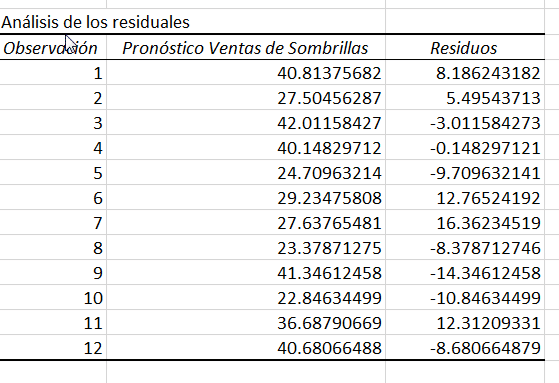
Estimado: 40.8 (calculado anteriormente) con relación al primer mes.
También puedes ver como sacar desviación estándar en Excel